前端算法

树

一种分层数据的抽象模型 js 中没有树，但可以用Object和Array构建树

树的深度优先遍历

尽可能深的搜索树的分支

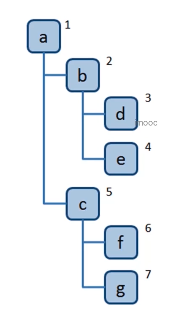
• 访问根节点
• 对根节点的 children 挨个进行深度优先遍历

const dfs = (root) => {
  console.log(root.val);
  root.children.forEach(dfs);
};

树的广度优先遍历

访问离根节点最近的节点

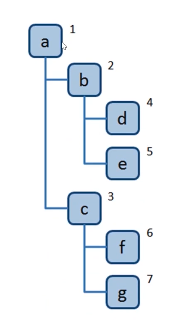
• 新建一个队列，把根节点入队
• 把对头出队并访问
• 把队头的 children 挨个入队
• 重复第 2、3 步，直到队列为空

const bfs = (root) => {
  const q = [root];
  while (q.length > 0) {
    const n = q.shift();
    console.log(n.val);
    n.children.forEach((child) => {
      q.push(child);
    });
  }
};

二叉树的先中后序遍历

二叉树的先序遍历

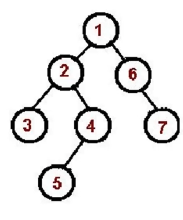
• 访问根节点
• 对根节点的左子树进行先序遍历
• 对根节点的右子树进行先序遍历

const preorder = (root) => {
  if (!root) return;
  console.log(root.val);
  preorder(root.left);
  preorder(root.right);
};

非递归版

const preorder = (root) => {
  if (!root) return;
  const stack = [root];
  while (stack.length) {
    const n = stack.pop();
    console.log(n.val);
    if (n.right) stack.push(n.right);
    if (n.left) stack.push(n.left);
  }
};

二叉树的中序遍历

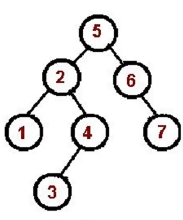
• 对根节点的左子树进行中序遍历
• 访问根节点
• 对根节点的右子树进行中序遍历

const inorder = (root) => {
  if (!root) return;
  inorder(root.left);
  console.log(root.val);
  inorder(root.right);
};

非递归版

const inorder = (root) => {
  if (!root) return;
  const stack = [];
  let p = root;
  while (stack.length || p) {
    while (p) {
      stack.push(p);
      p = p.left;
    }
    const n = stack.pop();
    console.log(n.val);
    p = n.right;
  }
};

二叉树的后序遍历

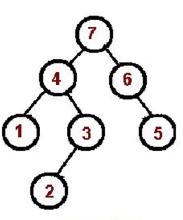
• 对根节点的左子树进行后序遍历
• 对根节点的右子树进行后序遍历
• 访问根节点

const postorder = (root) => {
  if (!root) return;
  postorder(root.left);
  postorder(root.right);
  console.log(root.val);
};

非递归版

const postorder = (root) => {
  if (!root) return;
  const outputstack = [];
  const stack = [root];
  while (stack.length) {
    const n = stack.pop();
    outputstack.push(n);
    if (n.left) stack.push(n.left);
    if (n.right) stack.push(n.right);
  }
  while (outputstack.length) {
    const n = outputstack.pop();
    console.log(n.val);
  }
};

数组-排序算法

冒泡排序（时间复杂度 O(n^2)）

动画图解

• 比较所有相邻元素，如果第一个比第二个大，则交换它们。
• 一轮下来，可以保证最后一个数是最大的。
• 执行 n-1 轮，就可以完成排序。

const bubbleSort = (arr) => {
  for (let i = 0; i < arr.length - 1; i++) {
    for (let j = 0; j < arr.length - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
};
bubbleSort([5, 4, 3, 2, 1]);

选择排序 (时间复杂度： O(n^2))

动画图解

• 找到数组中的最小值，选中它并将其放置在第一位。
• 接着找到第二小的值，选中它并将其放置在第二位。
• 以此类推，执行 n-1 轮。

const selectionSort = (arr) => {
  for (let i = 0; i < arr.length - 1; i++) {
    let indexMin = i;
    for (let j = i; j < arr.length; j++) {
      if (arr[j] < arr[indexMin]) {
        indexMin = j;
      }
    }
    if (indexMin !== i) {
      [arr[i], arr[indexMin]] = [arr[indexMin], arr[i]];
    }
  }
  return arr;
};
selectionSort([5, 4, 3, 2, 1]);

插入排序 (时间复杂度： O(n^2))

动画图解

• 从第二个数开始往前比。
• 比它大就往后排。
• 以此类推进行到最后一个数。

const insertionSort = (arr) => {
  for (let i = 1; i < arr.length; i++) {
    const temp = arr[i];
    let j = i;
    while (j > 0) {
      if (arr[j - 1] > temp) {
        arr[j] = arr[j - 1];
      } else {
        break;
      }
      j--;
    }
    arr[j] = temp;
  }
  return arr;
};
insertionSort([5, 4, 3, 2, 1]);

归并排序 (时间复杂度： O(n*logn))

火狐浏览器的排序原理

动画图解

• 分：把数组劈成两半，再递归地对子数组进行“分”操作，直到分成一个个单独的数。
• 合：把两个数合并为有序数组，再对有序数组进行合并，直到全部子数组合并为一个完整数组。

const mergeSort = (arr) => {
  if (arr.length === 1) {
    return arr;
  }
  const mid = Math.floor(arr.length / 2);
  const left = arr.slice(0, mid);
  const right = arr.slice(mid, arr.length);
  const orderLeft = mergeSort(left);
  const orderRight = mergeSort(right);
  const res = [];
  while (orderLeft.length || orderRight.length) {
    if (orderLeft.length && orderRight.length) {
      res.push(
        orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift()
      );
    } else if (orderLeft.length) {
      res.push(orderLeft.shift());
    } else if (orderRight.length) {
      res.push(orderRight.shift());
    }
  }
  return res;
};
mergeSort([5, 4, 3, 2, 1]);

快速排序 (时间复杂度： O(n*logn))

火狐浏览器的排序原理

动画图解

• 分区：从数组中任意选择一个“基准”，所有比基准小的元素放在基准前面，比基准大的元素放在基准的后面。
• 递归：递归地对基准前后的子数组进行分区。

const quickSort = (arr) => {
  if (arr.length <= 1) {
    return arr;
  }
  const left = [];
  const right = [];
  const mid = arr[0];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] < mid) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return [...quickSort(left), mid, ...quickSort(right)];
};
quickSort([5, 4, 3, 2, 1]);

数组-搜索算法

顺序搜索（时间复杂度 O(n)）

动画图解

• 遍历数组。
• 找到跟目标值相等的元素，就返回它的下标。
• 遍历结束后，如果没有搜索到目标值，就返回-1。

const sequentialSearch = (arr, item) => {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === item) {
      return i;
    }
  }
  return -1;
};
sequentialSearch([5, 4, 3, 2, 1], 3);

二分搜索（时间复杂度 O(logN)）

动画图解

• 从数组的中间元素开始，如果中间元素正好是目标值，则搜索结束。
• 如果目标值大于或者小于中间元素，则在大于或小于中间元素的那一半数组中搜索。

const binarySearch = (arr, item) => {
  let low = 0;
  let high = arr.length - 1;
  while (low < high) {
    const mid = Math.floor((low + high) / 2);
    const element = arr[mid];
    if (element < item) {
      low = mid + 1;
    } else if (element > item) {
      high = mid - 1;
    } else {
      return mid;
    }
  }
  return -1;
};
binarySearch([1, 2, 3, 4, 5], 3);